Q:

I need to construct a 12-sided figure with a certain radius. How do I find the length of one of its sides?

Dennis R. Burr, Lumby, None

A:

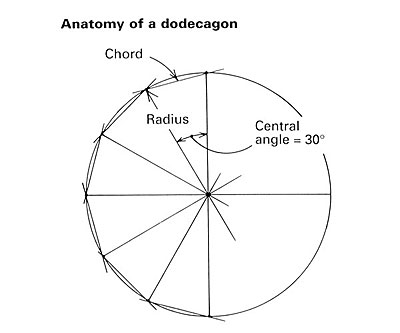
Rich Ziegner responds: I assume you’re talking about a regular 12-sided figure, where all sides are of equal length. If this regular 12-sided figure (called by the ancient Greeks a dodecagon, meaning a regular 12-sided figure) were inscribed within a circle, you’d then be looking for the length of any one of 12 chords (see drawing). You already know the radius, so finding the length of a chord is a simple matter of: chord = [sine(central angle/2)] x 2radius.

Great, you say, but what does it mean? It means that any side of your dodecagon, when it’s sliced into 12 triangles, equals the sine of one-half the central angle multiplied by twice the radius.

So first we need to know the size of the central angle. To find the central angle of any regular polygon, 12-sided or otherwise, divide the number of sides into the number of degrees in a circle: 360. In this case, 360° divided by 12 is 30°. Therefore, your central angle is 30°. Divide it in half as the formula requires, and you get 15°. Are you still awake?

You can get the sine of a given angle from an algebra book, a scientific calculator or a really nerdy guy with tape on his glasses. The sine of 15° is .2588.

Because you don’t say what the radius is, I’ll pick a nice round figure: 10m (for those of you still unfamiliar with the metric system, a meter is something at the side of the road that you put quarters into when you park your car beside it).

Now let’s plug the numbers into the formula: chord = [sine15°] x [2 x 10]. Sine15° is .2588 and twice 10 is 20, so multiply .2588 by 20, and you find that the length of one side of a dodecagon inscribed in a circle with a 10m. radius is 5.176m.

By the way, I found this equation in a book by Johnny and Margaret Hamilton called Math to Build On (Construction Trades Press, 1993; see FHB #85, pp. 132, for a review).