Roof Framing Simplified
This direct approach involves full-size layouts and stringing rafter lines.
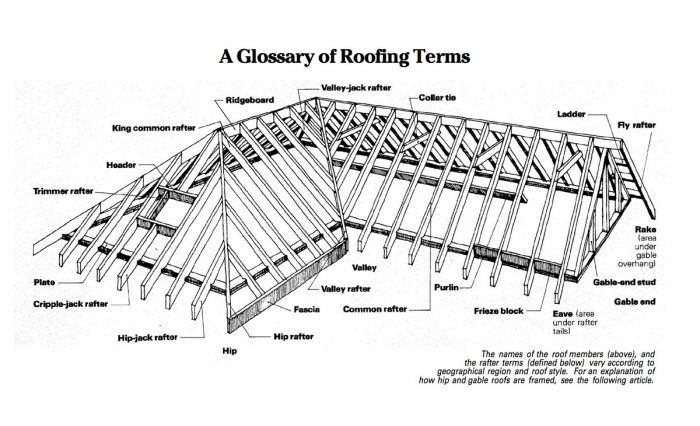
Synopsis: The author briefly explains two methods of framing a roof that do not involve mathematical calculations: snapping chalk lines on the subfloor and taking measurements directly from the roof. An accompanying glossary identifies various components of a framed roof.
There isn’t a cut in roof framing that can’t be calculated given a sharp pencil, a framing square and a head for math. But my 20 years in the trade have taught me that in some cases, the theoretical calculation of rafter angles and lengths is slower and leaves more room for error. While I think that it’s important to understand the geometry of roof framing, the empirical method can save time and frustration, and contribute to your understanding of the process. I’m better at solving problems when I can grasp them — literally.
When I’m cutting a complicated roof and things get foggy, I use two techniques to help me produce rafters that fit the first time. I chalk lines on the plywood subfloor to represent a rafter pair in relation to its plates and ridge. This two-dimensional diagram is laid out full size. Pattern rafters can be tested right there on the job site. The other method I use is to deal directly with the components involved by getting up on the roof and measuring the relationships between the rafter to be cut and the existing plate and ridge with string and sliding bevel.
I used this method several years ago when I built a Y-shaped house. One wing was for the bedrooms and the other contained the kitchen, dining room and family room. The stem of the Y was the living room. The roof over the wings called for trusses, but the living-room rafters were exposed. The problem was in framing the intersection of the three roofs. These beams were big, long and expensive, and all the cuts would show. Had the house been a T shape, the valley rafters would have been a textbook case, and I could have found the information I needed in the rafter tables on my framing square. But since the intersection was 120° and not 90°, I had to find the angles by calculation or direct observation. I chose the latter.
Full-size layout
After setting the trusses, I chalked a full-size layout of the living-room common rafters and ridge on the subfloor below. The ridge beam was a 4×14, and the common rafters were 4x8s on 4-ft. centers. I decided to tackle the easiest steps first. This gave me time to think about the problem while reducing the parts in the puzzle.
The ridge beam went up first. I found its height by measuring on the full-size layout. The common rafters were then cut using patterns made from the layout. I nailed these in place starting at the outside wall, working toward the junction of the Y.
The valley rafter was next. Its location is shown above. Valley rafters are usually heftier than common rafters because they have a longer span, and have to carry the additional weight of the valley jacks. In this case, the valley rafter was a 4×10. Because it’s deeper, to achieve the same height above the plate and ridge, its seat and ridge cuts also differed from hose of the common rafters. I found it faster and easier to measure the actual distances than to calculate imaginary ones. This way I could find the length of the rafter and the angles of the cuts without guesswork or error. This took me back up on the roof armed with a ball of nylon string, a sliding bevel and a level…
For more photos, drawings, and details, click the View PDF button below to read the entire article:
Fine Homebuilding Recommended Products
Fine Homebuilding receives a commission for items purchased through links on this site, including Amazon Associates and other affiliate advertising programs.

Original Speed Square

Roof Jacks

Leather Tool Rig





