How it Works: Simple Wood Beams

Synopsis: Beams are critical to the structure of a house. Here, R. Bruce Hoadley explains how they support building loads, and he demonstrates how changes to the length, width, and depth of a beam affect its load-bearing capacity and deflection. Read the full article with detailed diagrams in the PDF below.

Beams, defined as elongated members that are loaded perpendicular to their long axis, are critical to the structure of a house. The classic example of a double or triple 2x beam supporting floor joists usually comes to mind, but joists, roof rafters, headers over windows and doors, and stair stringers are all examples of beams.

Today, builders often rely on engineered structural lumber— LVLs, PSLs, I-joists, and others—but dimensional lumber is still used widely as well. In practice, builders have no say over the strength of the wood itself; we are simply charged with using the inherent strength effectively.

If you know the limit of acceptable deflection and how much weight a beam needs to carry—both of which are provided by building codes—then the type, species, grade, length, width, and depth of the beam all can be selected.

Simple Wood Beams

Although engineers are invaluable for their knowledge of the calculations used to specify beams of all sorts—including more complicated setups such as continuous, fixed-end, and cantilever beams—anyone can apply the principles of beam mechanics generally, without getting into precise calculations, to improve the mechanical performance of countless parts of a house. The decision of where to place a support column or partition wall, when to choose double 2x8s as opposed to a single 2×10, and the most effective method for stiffening an under size joist can benefit from a basic understanding of the relationship between a beam’s carrying capacity and its stiffness. Here’s how it works.

Know your beam options

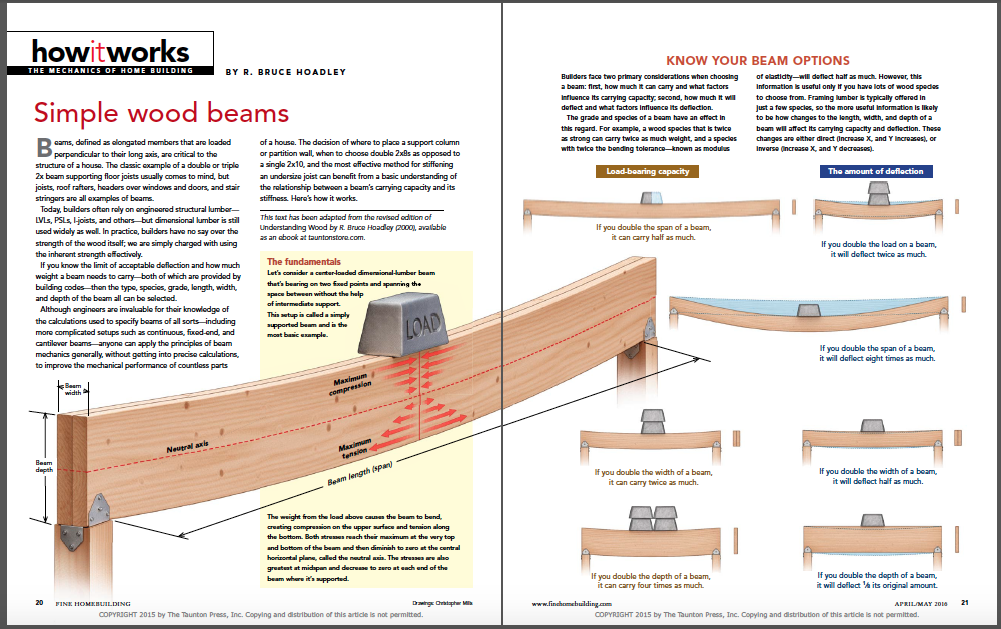
Builders face two primary considerations when choosing a beam: first, how much it can carry and what factors influence its carrying capacity; second, how much it will deflect and what factors influence its deflection.

The grade and species of a beam have an effect in this regard. For example, a wood species that is twice as strong can carry twice as much weight, and a species with twice the bending tolerance —known as modulus of elasticity—will deflect half as much. However, this information is useful only if you have lots of wood species to choose from. Framing lumber is typically offered in just a few species, so the more useful information is likely to be how changes to the length, width, and depth of a beam will affect its carrying capacity and deflection. These changes are either direct (increase X, and Y increases), or inverse (increase X, and Y decreases).

The fundamentals

Let’s consider a center-loaded dimensional-lumber beam that’s bearing on two fixed points and spanning the space between without the help of intermediate support. This setup is called a simply supported beam and is the most basic example.

The weight from the load above causes the beam to bend, creating compression on the upper surface and tension along the bottom. Both stresses reach their maximum at the very top and bottom of the beam and then diminish to zero at the central horizontal plane, called the neutral axis. The stresses are also greatest at midspan and decrease to zero at each end of the beam where it’s supported.

For more diagrams and details on the fundamentals of simple wood beams, click the View PDF button below. 

From Fine Homebuilding #258

Fine Homebuilding Recommended Products

Fine Homebuilding receives a commission for items purchased through links on this site, including Amazon Associates and other affiliate advertising programs.

Stabila Extendable Plate to Plate Level

This level raises the bar for accuracy and quality. The extensions are designed to contact and plumb from bottom to top plates, avoiding studs that may be bowed.

Buy at Amazon

Stabila Classic Level Set

Plumb and level are the hallmarks of good craftsmanship, so having a complete set of professional levels on the job is crucial to success.

Buy at Amazon

Tajima Chalk Rite Chalk Line

Snapping a line should be quick, clean, and accurate, and the Tajima certainly doesn’t disappoint. It’s pro-grade and works as advertised.

Buy at Amazon